Ray-tracing analytical absorption correction for X-ray crystallography based on tomographic reconstructions.
Lu, Y., Duman, R., Beilsten-Edmands, J., Winter, G., Basham, M., Evans, G., Kamps, J.J.A.G., Orville, A.M., Kwong, H.S., Beis, K., Armour, W., Wagner, A.(2024) J Appl Crystallogr 57: 649-658
- PubMed: 38846772
- DOI: https://doi.org/10.1107/S1600576724002243
- Primary Citation of Related Structures:
8QUQ, 8QUR, 8QUU, 8QUV, 8QUZ, 8QVB, 8QVS, 8QVV - PubMed Abstract:
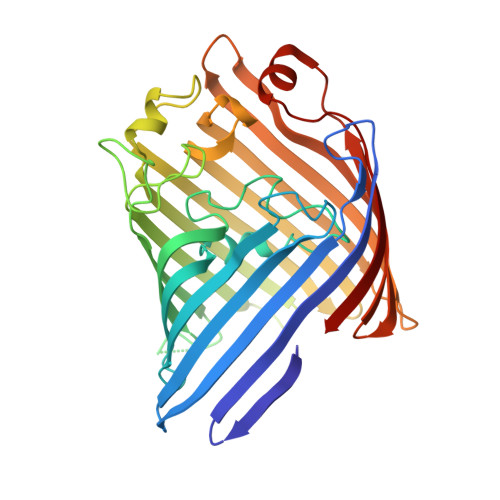
Processing of single-crystal X-ray diffraction data from area detectors can be separated into two steps. First, raw intensities are obtained by integration of the diffraction images, and then data correction and reduction are performed to determine structure-factor amplitudes and their uncertainties. The second step considers the diffraction geometry, sample illumination, decay, absorption and other effects. While absorption is only a minor effect in standard macromolecular crystallography (MX), it can become the largest source of uncertainty for experiments performed at long wavelengths. Current software packages for MX typically employ empirical models to correct for the effects of absorption, with the corrections determined through the procedure of minimizing the differences in intensities between symmetry-equivalent reflections; these models are well suited to capturing smoothly varying experimental effects. However, for very long wavelengths, empirical methods become an unreliable approach to model strong absorption effects with high fidelity. This problem is particularly acute when data multiplicity is low. This paper presents an analytical absorption correction strategy (implemented in new software AnACor ) based on a volumetric model of the sample derived from X-ray tomography. Individual path lengths through the different sample materials for all reflections are determined by a ray-tracing method. Several approaches for absorption corrections (spherical harmonics correction, analytical absorption correction and a combination of the two) are compared for two samples, the membrane protein OmpK36 GD, measured at a wavelength of λ = 3.54 Å, and chlorite dismutase, measured at λ = 4.13 Å. Data set statistics, the peak heights in the anomalous difference Fourier maps and the success of experimental phasing are used to compare the results from the different absorption correction approaches. The strategies using the new analytical absorption correction are shown to be superior to the standard spherical harmonics corrections. While the improvements are modest in the 3.54 Å data, the analytical absorption correction outperforms spherical harmonics in the longer-wavelength data (λ = 4.13 Å), which is also reflected in the reduced amount of data being required for successful experimental phasing.
Organizational Affiliation:
Oxford e-Research Centre, Department of Engineering Science, University of Oxford, 7 Keble Road, Oxford OX1 3QG, United Kingdom.